Algorithms 구성

• Algorithms (1) - Machine learning basic 기초
• Algorithms (2) - Machine learning linear regression (1)
• Algorithms (2) - Machine learning linear regression (2)
• Algorithms (2) - Machine learning linear regression (3)
• Algorithms (2) - Machine learning linear regression (4)
• Algorithms (3) - Machine learning logistic regression (1)

Parameter Estimation Algorithms

Least squared estimator

• estimator: a function of the samples
• purpose of estimator: to find out unknown parameters
• types of estimator
  1. point estimator (점 추정)
  2. interval estimator (구간 추정)

point estimator

Yi = w0 + w1 Xi + εi, εi ~ N(0, σ²), i = 1, 2, … n

• w0 에 대한 point estimator: ^w0 = mean(y) - ^w1 * mean(x)
• w1 에 대한 point estimator: linear regression 2 참조
• σ²에 대한 point estimator: ^σ²= (1 / n - 2) sum ( ei²) -> residual

Interval Estimation

• 구간으로 측정하여 보다 유연한 정보 제공
• θ (parameter)에 대한 구간 측정 -> ^θ - 상수값 * std(θ) <= θ <= ^θ + 상수값 * std(θ)

기울기에 대한 가설검정

• unknown parameter에 대한 가설을 세우고 이를 검정

p-value

• p-value가 0.05나 0.01보다 작으면 reject null hypothesis

statsmodels.formula.api에 ols function을 통한 모델링을 했을때

• parameters: wet, frs, cld, intercept
• point estimates: 각각의 coef
• std: 각각의 std err

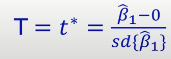
• t: 전반적으로 모든 parameters들의 abs(t)값이 > 1.96 (p < 0.05) 또는 abs(t) > 2.58 (p < 0.01) 큼 -> null hypothesis를 reject

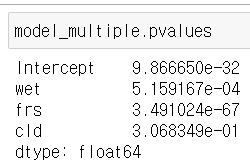
• p-value: 모든 slope parameters이 0.05보다 큰 값이 없기 때문에 statistically significant