Machine Learning Algorithm - logistic regression (1)
Algorithms 구성
- Algorithms (1) - Machine learning basic 기초
- Algorithms (2) - Machine learning linear regression (1)
- Algorithms (2) - Machine learning linear regression (2)
- Algorithms (2) - Machine learning linear regression (3)
- Algorithms (2) - Machine learning linear regression (4)
- Algorithms (3) - Machine learning logistic regression (1)
Logistic regression (classification)
- y (output)가 범주형 data 일때 사용 (categorical y)
- 분류예측을 하는 모델링
- 제품이 불량인지 분류
- 코로나가 걸렸는지 안걸렸는지 등
- parameter들을 가지고 y값을 predict 하여 분류하는 model
Bernoulli random variable
Yi = B0 + B1 Xi + ei; Yi = 0 or 1
- assume E(ei) = 0 -> Yi = B0 + B1 Xi
- P(Yi = 1) = prob_x 라고 가정할때
- P(Yi = 0) = 1 - prob_x 로 나타낼수 있다
- E(Yi) = 1 * prob_x + 0 * (1 - prob_x) = prob_x
- E(Yi) = B0 + B1 Xi = prob_x
x 값이 주어졌을 때 y값이 1을 가질 확률로 표현하는 모델링
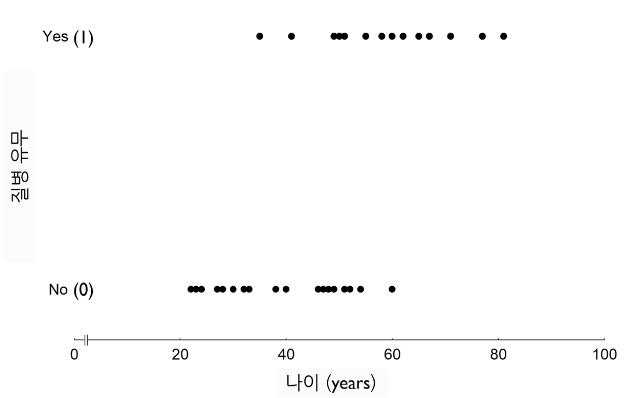
이런 data를 linear regression으로 fitting하기에는 적합하지 않다.
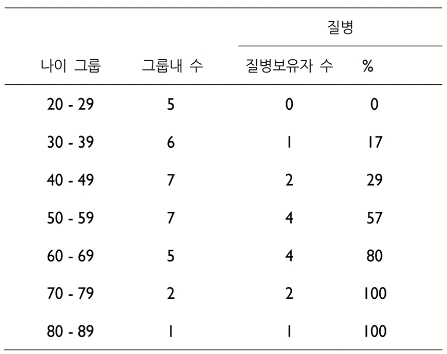
- 나이별로 그룹을 만들고 질병을 보유하고 있는 확률을 계산
- 그래프로 표시하면 빨간색 선이 파란색 linear regression보다 더 정확한 line이다.
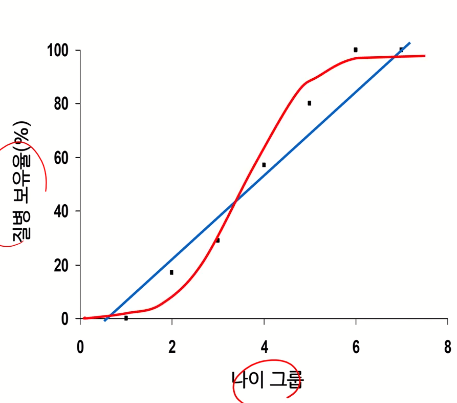
이런 관계를 나타낼수 있는 함수가 Logistic 함수 혹은 sigmoid 함수라고 한다.

- 항상 f(x)는 0과 1 사이임
parameter x가 범주 1에 속할 확률이 logistic function
- E(y) = P(X = x) = P(Y = 1 given X = x) = 1 - P(Y = 0 given X = x)
이렇게도 표현이 가능하다
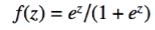
- “logistic” function
where z = B0 + B1X
parameter B0 과 B1이 y값과 linear relationship이 아니라서 직관적인 해석이 안된다
그래서 odd 개념을 접목시켜야된다
odds (승산)
성공확률을 p라고 정의할때 실패 대비 성공 확률 비율
- odd = p / (1 -p)
ex) 월드컵에서 프랑스가 이길 odd가 2 / 11이라면 p/(1 - p)가 2/11이므로 p로 풀어내면 p = 2/13인 0.15 (15%)가 된다
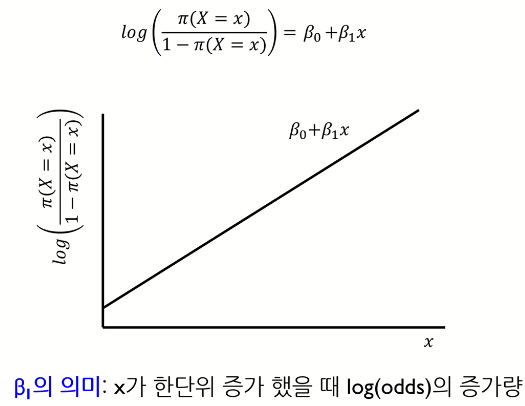
odds의 개념을 logistic에 접목을 시키면 이런식으로 표현이 가능하다
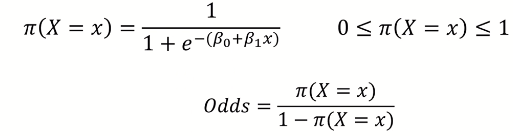
odd에다가 log를 취하면 단순환 선형 결합의 형태로 바뀐다. (logit transformation)
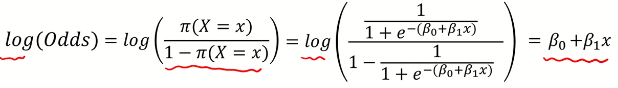
여기서는 B1에 대한 해석이 직관적으로 바뀜 (x가 증가하면 log(odd)가 증가함; x가 증가함에 따라 성공확률이 log scale로 얼마만큼 증가했다라고 할 수 있다)