Algorithms 구성

• Algorithms (1) - Machine learning basic 기초
• Algorithms (2) - Machine learning linear regression (1)
• Algorithms (2) - Machine learning linear regression (2)
• Algorithms (2) - Machine learning linear regression (3)
• Algorithms (2) - Machine learning linear regression (4)
• Algorithms (3) - Machine learning logistic regression (1)

결정계수 (coefficient of determination: R^2)

• Yi = 실제 Y 값
• 두번째 점은 모델링에서 나온 ^Y값
• Y bar은 실제 Y값의 평균값

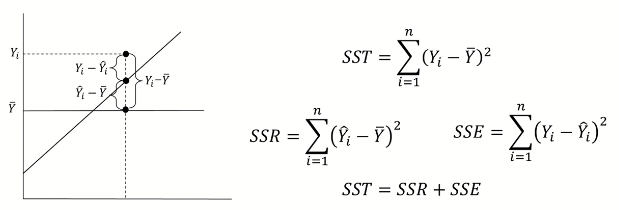
R^2

• SSE = 실제 Y값과 모델의 ^Y 값들의 차이의 제곱 합 (Residual sum of squares와 같은 맥락)
• SST = 모델의 ^Y값과 실제 Y의 평균값과의 차이의 제곱 합
• SST = RSS + ESS

RSS / TSS = R^2

• 1인 경우: SST = SSR + (SSE = 0); model의 직선이 실제 Y값들을 지나감 (확정적인 관계) 현재 가지고 있는 x변수로 y를 100% 설명, 모든 y가 linear regression line위에 있다

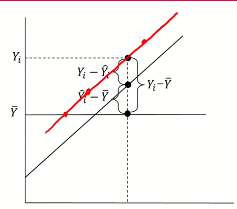
• 0인 경우: SST = (SSR = 0) + SSE; model의 직선이 Y값의 평균을 지나감 (parameter x가 아무런 y에 효과가 없음) 현재 가지고 있는 x변수는 y를 설명(예측)에 전혀 도움이 되지않는다

1. 사용하고 있는 x변수가 y변수의 variance를 얼마나 줄였는지 정도
2. 단순히 y의 평균값을 사용했을 때 대비 x정보를 사용함으로써 얻는 성능 향상 정도

수정 결정계수 (Adjusted R^2)

• R^2는 의미없는 변수 x가 추가되어도 항상 증가한다
• 수정 R^2는 의미없는 변수 x가 추가되었을때 R^2가 증가하는것을 방지하기위해 특정 계수를 식앞에 곱해줌
• 의미있는 변수 x가 추가되었을때는 SSE값이 떨어지기 때문에 전체 adj R^2는 증가하게 된다

예제

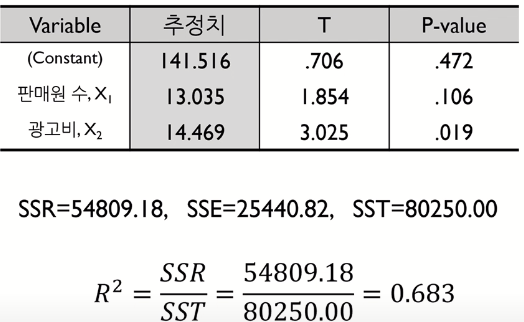
• parameter x1 (판매원 수)와 x2 (광고비) 에 의해 y (매출액)의 variance가 68.3% 감소
• 매출액의 평균 (y bar)에 대비 x1, x2 parameter를 이용하면 설명력이 68.3% 증가
• 현재 분석에 사용하고 있는 판매원 수와 광고비는 “변수 품질”정도가 68.3 (100점 기준)

분산 분석 (analysis of variance)

RSS / ESS (x 변수에 의해 설명된 것 / 에러에 의한 설명된 것)

• SSR / SSE > 1
  1. RSS > ESS; x변수가 y변수에 statistically significant
  2. x변수의 기울기가 0이 아님 -> reject null hypothesis
• 0 <= SSR / SSE <= 1
  1. SSR < SSE; x변수가 y변수에 not statistically significant
  2. x변수의 기울기가 0 -> null hypothesis is true